Paper Explainer: Geometry and Stability of Supervised Learning Problems

Just released a new paper! In it, my coauthors and I try to make sense of some challenges in machine learning by creating a "space of all problems". If you don't know what that means, that's okay! This post explains the big ideas for non-mathematicians.

 

What is Supervised Learning?

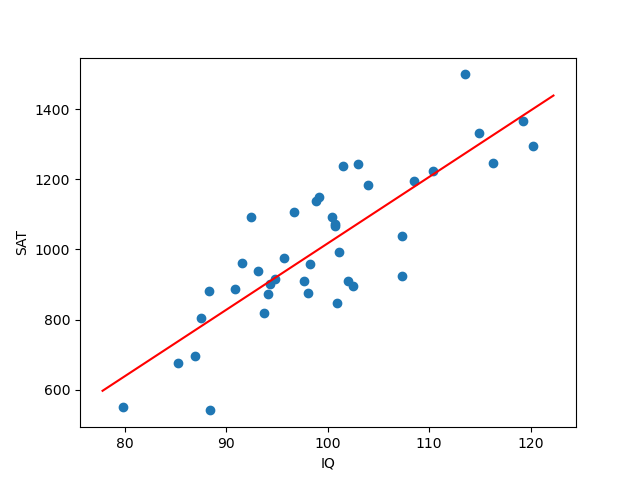
Suppose you've got some data on the IQ and SAT scores of a bunch of people, and the data looks like this:

 

(Note: I made this data up. Don't believe it.) Using this data, can you use someone's IQ score to get a rough estimate for their SAT score? Sure, you could fit a trendline to the data using some good ol' linear regression. It'll look something like this:

Now if you know someone's IQ (say, 110), you can predict what their SAT score might be using the trendline (in this case, about 1207).

Congratulations! You just took part in supervised learning! You used an algorithm to...

1. take data about the relationship between two variables $x$ and $y$, and
2. use that data to choose a prediction function that maps any known $x$ to a prediction for $y$.

For the most part, that's all that supervised learning is! Everything from linear regression to neural networks follows this same basic blueprint. Of course, neural networks use more complicated data to select fancier functions, but at heart it's the same idea. (There are some extra details in supervised learning, like "How do I pick the actual function?" and "How do I know my chosen function is a good fit?" These are details we won't need to worry about here.)

 

The "learning" in supervised learning is there because the algorithm is "learning" the relationship between your input and output variables, such as IQ and SAT scores. The "supervised" part is because the examples you give to the algorithm come with the correct answers. Each data point is an example input (the $x$ value) together with the "correct answer" (the $y$ value). The algorithm tries to come up with a relationship that matches the correct answers as closely as possible. If, instead, your algorithm just took a bunch of $x$ values and tried to find patterns without knowing the $y$ values, that would be an example of unsupervised learning, which we won't get into here.

Supervised Learning Headaches

Let's say you sit down to work on a supervised learning problem. In a perfect world, you would...

• Have access to unlimited amounts of data
• Have data with no noise or inaccuracies
  
• Formulate the problem in a mathematically elegant way without having to worry about how hard anything is to compute
• Be able to select the function that represents the actual true relationship between the inputs and outputs.

In practice, of course, you get none of these things. You instead must...

• Make the best of less data than you want
• Use noisy or inaccurate data
• Approximate your elegant math with simpler math that is easier for computers to work with
  
• Guess what kind of function will be a good fit and narrow your attention to those
  

For instance, in the IQ/SAT example above, we had very little data (only 40 points). Our data might be inaccurate because people might misremember, round, or embellish their scores. Or maybe the data is inaccurate because I asked people on, say, a college campus, who will tend to have higher test scores than the general population. Also, when we decided to fit a trendline, we were narrowing our focus to only linear functions. If the true relationship between the input and output doesn't look like a straight line, this is a serious limitation.

We could actually think of these as two different problems. First there is the ideal, perfect-world problem. This is the problem you want to solve. There is also the corrupted, imperfect, real-world problem, which is the problem you get to solve. The problem you want to solve is certainly different than the problem you get to solve. How different will depend on the magnitude of the noise, bias, etc. We know that the ideal and actual problems are different, but we'd like some kind of guarantee that they aren't too different.

Now, there's a lot of research on how much a certain compromise will change a problem. "If I add X amount of Y kind of noise to a problem, it will change the problem in Z way." Things like that. But those results tend to be pretty specific. They're about what happens to a problem if you change one thing about the problem. But that's not how it works in the real world; you gotta accept a whole bunch of compromises at once. Is there a good way to think about making a whole bunch of changes to your problem at once?

Thinking with Geometry

Let's think about all these changes geometrically. Here's a picture (adapted from the paper) to help us do so:

 

We start with the "ideal problem" on the left. That's the perfect problem we'd like to get our hands on. Each compromise, represented by the red arrows, pushes the problem a little bit in some direction. Adding noise? That changes the problem. Approximating some hard math with easier math? That changes the problem too. Each of these changes push the problem, and those pushes add up, leaving us with the "actual problem" in the upper right.

This picture is a helpful visualization, but kind of vague. If we could make actual mathematical sense of this picture, we could use geometry to make sense of the difference between the ideal problem and the actual problem.

 

This is exactly what we do in the paper! We invent the space of supervised learning problems, in which each point represents a different problem. In particular, the "ideal problem" and "actual problem" are represented by points in this big space, just like in the picture above. Want to know how different those two problems are? Well, if you've got a good idea about how long each of the red arrows are, you've got a good idea about how far apart the problems can be! Geometry solves the problem!

 

Here's the reason this is really useful: any kind of change to a problem could be represented with a red arrow. And you can chain together any number of the red arrows. So our framework can handle all sorts of simultaneous changes to a problem.

What's Actually in the Paper?

For anyone interested, we'll get into the technical weeds just a little bit more to explain how we did any of this. In the paper, we invent the space of supervised learning problems. To actually pull this off, we take inspiration from another field of math called optimal transport. The name sounds pretty dry, but that's just because it's a field of math that was founded to deal with problems in economics, and economists are famously dry people. All that you need to know about optimal transport is that it turns out to be really useful for doing geometry on things that don't obviously have any geometry going on. Anybody can do geometry in 2D space, but only with optimal transport can you do geometry in, for instance, the space of spaces themselves! Very meta! Very cool!

Anyway, the good people in optimal transport theory have a tried-and-true method for putting geometry where it doesn't belong. All we have to do is apply this method to supervised learning problems and presto! We've unlocked the power of geometry!

 

Most of the actual paper is dedicated to developing this geometry on the space of all supervised learning problems and showing that the geometry isn't weird. Specifically, we prove that...

1. problems you'd expect to be close together actually are in our geometry, and
2. problems that are close together under our geometry really do deserve to be called "similar".

If you're interested in more details, check out the paper! The whole thing is pretty long, but the introduction is a more technical overview of the paper and it's short.

Thanks for reading!