The Logarithmic Black Sheep
Behold, the integral power rule:
For any real $p$,
$$\int x^p\, dx = \frac{1}{p+1} x^{p+1} +C$$
Dependable. Ubiquitous. Cursed with an asterisk:
... unless $p=-1$, in which case
$$\int x^p\, dx = \ln(x)+C.$$
I have gotten used to this fact through years of working with integrals. All the same, it bothers me. Every time I am forced to check if my exponent falls into this one exceptional case, a voice somewhere in my head protests. "How does this make sense?? How do you get a continuous family of monomials except for the one case where, of all things, you get a logarithm!?"
This is not to say I don't understand why $\int dx/x$ spits out a logarithm. I can see that the usual formula would force you to divide by 0 at $p=-1$, and I could even prove the antiderivative in a few lines. It's just that it feels like an unexplained discontinuity at a point. I never learned how this logarithmic black sheep fits in with the big happy family of monomials.
Fitting the Logarithm into the Family
I determined today that I was going to figure this out. Can I make sense of this exceptional case? So I did what everyone should do when they are confused by real-valued functions: I opened Desmos. My first question was this: does the formula from the power rule converge in some way to $ln$ as $p\to -1$? So I made a few graphs. I plotted the formula from the power rule
$$
f_p(x) = \frac{1}{p+1}x^{p+1}
$$
adding a slider for $p$, and plotted $\ln(x)$ as well for comparison. I pulled that slider for $p$ slowly to the left towards -1 and...
https://www.desmos.com/calculator/wn89lk2l44
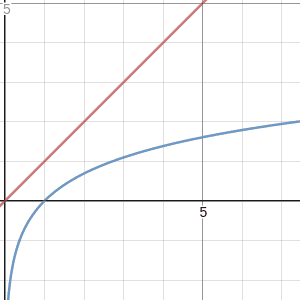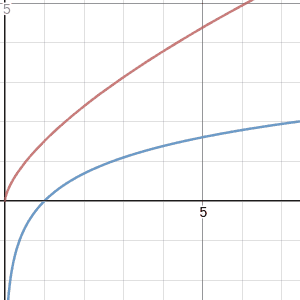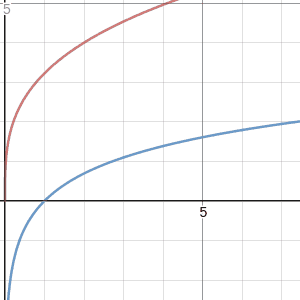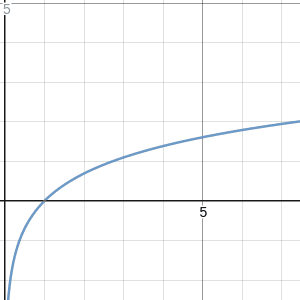
I can hear a slide whistle when I watch that gif. It definitely diverges at every positive $x$. I mean, why wouldn't it? The $x^{p+1}$ term is approaching $x^0=1$ while the denominator is going to 0, blowing the fraction up to infinity. This function $f_p$ definitely does not converge to $\ln$ as $p\to -1$.
But something about the picture was still tickling at my brain. While the values were diverging, the shape of the graph DID seem to approximate the shape of the logarithm more and more as $p$ got closer to $-1$. The vertical placement of that distinctive shape just got less and less correct as $p$ approached its target. This is exactly the kind of problem that can be solved with one last trick up our sleeve: the arbitrary constant. While $f_p$ doesn't converge the way we want, maybe $f_p + C$ does converge for some choice of $C$. What we've done so far amounts to setting $C=0$. It might seem like adding a constant won't change the convergence, but remember that it just needs to be a constant with respect to $x$. We can make $C$ depend on $p$. To signify this, we'll refer to it as $C_p$.
So what value of $C_p$ do we choose to make $f_p(x) + C_p$ converge at all, hopefully to $\ln(x)$? We could just blindly try a few functions of $p$ to counteract the divergence, or we could be smart about it; what if we choose $C_p$ specifically so that $f_p +C_p$ always agrees with $\ln$ at some point? Anchor it down, so to speak. For instance, let's choose $C_p$ in a way that makes sure $f_p(1)+C_p = 0=\ln(1)$ for every $p$. If you solve for $C_p$ in this equation, you get $C_p = - 1/(p+1)$. Returning to our friend Desmos, we can plot
$$
f_p(x) + C_p = \frac{1}{p+1}x^{p+1} - \frac{1}{p+1}
$$
and compare it to $\ln(x)$. Lo and behold...
https://www.desmos.com/calculator/utomijzsssas we slide $p$ towards $-1$, we get a curve that lies tangent to $\ln$ at $x=1$, hugging it tighter and tighter as $p$ approaches its target. In other words, it appears that
$$
\lim_{p\to -1} f_p(x) + C_p = \ln(x)
$$
for all positive $x$. Indeed, this can be proven with a quick application of L'Hôpital's rule. The apparent discontinuity of our exceptional case at $p=-1$ was not exceptional at all; it appears as a natural choice if you only choose a nice value for the arbitrary constant! Our black sheep $\ln$ really does fit into this family of antiderivatives quite nicely!
Deducing the Exception Using the Rule.
We can go even further. Let's suppose we didn't know the antiderivative of $1/x$. Maybe we've figured out the general integral power rule, but aren't sure what to do when $p=-1$. We could actually use the above argument to prove that the answer is $\ln(x)$. (The reader that loses their way in this argument is welcome to skip to the "Ta-da!" a few paragraphs down.)
Let's try it out. The general integral power rule tells us that for any $x>0$,
$$
\int_1^x t^p\, dt = \left(\frac{t^{p+1}}{p+1}\right]_1^x = \frac{x^{p+1}}{p+1} - \frac{1}{p+1}.
$$
Aha! Our chosen constant $C_p$ from earlier appears by itself clear as day! We already argued that the limit of this expression as $p\to -1$ is $\ln(x)$. So
$$
\lim_{p\to -1}\int_1^x t^p\, dt = \ln(x)
$$
(The concerned reader may wonder if $\ln$ appears in the evaluation of that limit because we smuggled in our knowledge that the antiderivative of $1/x$ is $\ln(x)$, the very fact that we are trying to prove. This is not the case; $\ln(x)$ appears when applying L'Hôpital's rule in the derivative of $x^p$ with respect to $p$. The proof of this fact requires only that $\ln(x)$ is the inverse function to $e^x$ and no knowledge of the result we are proving.)
Now since $t^p$ converges uniformly to $t^{-1}$ between $x$ and 1 as $p\to -1$, we can interchange the integral and the limit to get
$$
\int_1^x t^{-1}\, dt = \int_1^x \lim_{p\to -1} t^p\, dt = \ln(x).
$$
Ta-da!
Of course, there is a much simpler proof that the antiderivative of $1/x$ is $\ln(x)$:
$$
\begin{aligned}
1 = \frac{d}{dx} x
& = \frac{d}{dx}e^{\ln(x)}
\\ &
= \frac{d}{dx}\ln(x) \cdot e^{\ln(x)} = \frac{d}{dx}\ln(x) \cdot x
\end{aligned}
$$
and dividing by $x$ gives that the derivative of $\ln(x)$ is $1/x$. This proof has the advantage of brevity and simplicity, since it uses only techniques that are familiar to Calculus students (the chain rule). Our proof above, however, provides something else.
Conclusion
Our new proof, while a bit longer, shows us something the shorter proof does not. It demonstrates that, not only does $\ln(x)$ fit into the family of monomial antiderivatives after all, it actually fits so nicely that we can deduce its existence just by considering the monomials around it. Not only is $\ln(x)$ not such a black sheep in the power integral rule, it is in fact the only function that can hold the whole collection of antiderivatives together as one big continuous family.

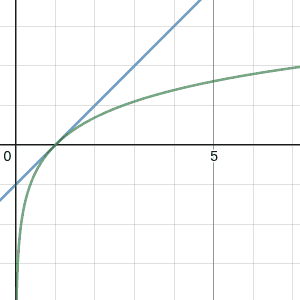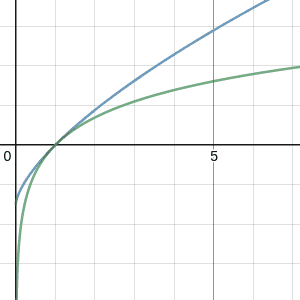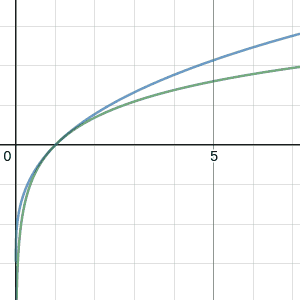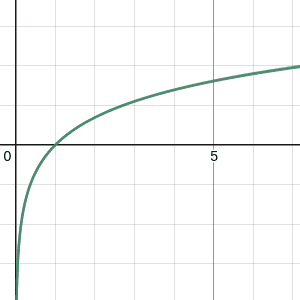


Thank you for this helpful explanation!!
ReplyDeleteGreat post... I got here from reddit (since you linked to this).
ReplyDelete